实现二叉查找树

Posted on |

二叉树每个节点的子节点不允许超过两个。通过将子节点的个数限定为 2，可以写出高效的程序在树中插入、查找和删除数据。

当考虑某种特殊的二叉树，比如二叉查找树时，确定子节点非常重要。二叉查找树是一种特殊的二叉树，相对较小的值保存在左节点中，较大的值保存在右节点中。

1
2
3
4
let nums = new BST()
nums.insert(56)
nums.insert(22)
nums.insert(81)

二叉查找树由节点组成，所以我们要定义的第一个对象就是 Node 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function Node(data, left, right) {
  this.data = data;
  this.left = left;
  this.right = right;
  this.show = show;
}

function show() {
  return this.data;
}

function BST () {
  this.root = null;
  this.insert = insert;
}

Node 对象既保存数据，也保存和其他节点的链接（ left 和 right ）， show() 方法用来显示保存在节点中的数据。

决定将节点放在哪个地方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function insert (data) {
  let n = new Node(data, null, null);
  if (this.root === null) {
    this.root = n;
  } else {
    let current = this.root;
    let parent;
    while (true) {
      parent = current;
      if (data < current.data) {
        current = current.left;
        if (current === null) {
          parent.left = n;
          break;
        }
      } else {
        current = current.right;
        if (current === null) {
          parent.right = n;
          break;
        }
      }
    }
  }
}

查找正确插入点的算法如下。

(1) 设根节点为当前节点。

(2) 如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点；反之，执行第 4 步。

(3) 如果当前节点的左节点为 null ，就将新的节点插入这个位置，退出循环；反之，继续执行下一次循环。

(4) 设新的当前节点为原节点的右节点。

(5) 如果当前节点的右节点为 null ，就将新的节点插入这个位置，退出循环；反之，继续执行下一次循环。

遍历二叉查找树

现在 BST 类已经初步成型，但是操作上还只能插入节点，我们需要有能力遍历 BST，这样就可以按照不同的顺序显示节点上的数据。

有三种遍历 BST 的方式：中序、先序和后序。

  1. 中序中序遍历按照节点上的键值，以升序访问 BST 上的所有节点。
  2. 先序遍历先访问根节点，然后以同样方式访问左子树和右子树。
  3. 后序遍历先访问叶子节点，从左子树到右子树，再到根节点。

中序遍历的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function inOrder(node) {
  if (!(node == null)) {
    inOrder(node.left)
    console.log(node.show());
    inOrder(node.right)
  }
}

let nums = new BST()
nums.insert(56)
nums.insert(22)
nums.insert(81)
nums.insert(10)
nums.insert(30)
nums.insert(77)
nums.insert(92)
inOrder(nums.root)

中序遍历方法的访问路径如下：10 22 30 56 77 81 92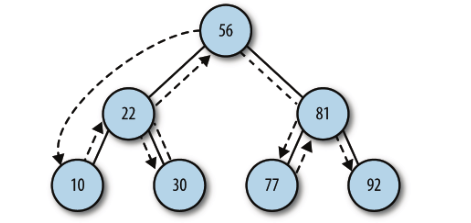

先序遍历的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function preOrder(node) {
  if (!(node == null)) {
    console.log(node.show());
    preOrder(node.left)
    preOrder(node.right)
  }
}

let nums = new BST()
nums.insert(50)
nums.insert(10)
nums.insert(70)
nums.insert(5)
nums.insert(15)
nums.insert(60)
nums.insert(80)
preOrder(nums.root)

先序遍历方法的访问路径如下：50 10 5 15 70 60 80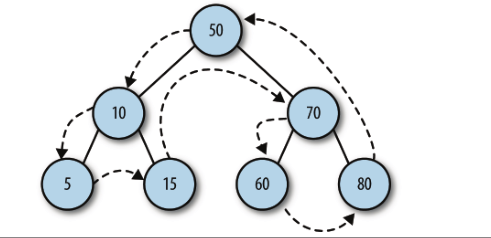

后序遍历的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function postOrder(node) {
  if (!(node == null)) {
    postOrder(node.left)
    postOrder(node.right)
    console.log(node.show());
  }
}

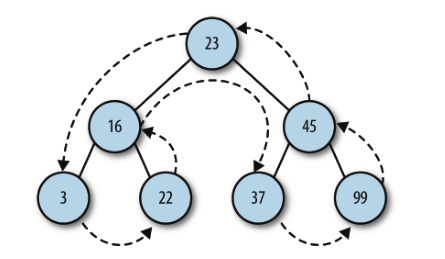
let nums = new BST()
nums.insert(23)
nums.insert(16)
nums.insert(45)
nums.insert(3)
nums.insert(22)
nums.insert(37)
nums.insert(99)
postOrder(nums.root)

后序遍历方法的访问路径如下：3 22 16 37 99 45 23